
Projet ANR JCJC HASCON (2019 - 2023)
Analyse Harmonique pour des Semigroupes sur des
Espaces Lp Commutatifs et Non-commutatifs
English version
Contact : 
Table des matières
1 Membres
- Cédric Arhancet
- Luc Deleaval
- Adrián González-Pérez (postdoctorant année universitaire 2019-2020)
- Christoph Kriegler (coordinateur du projet)
2 Mots clés de recherche
- Analyse harmonique
- Semigroupes d’opérateurs
- Géométrie non-commutative
- Calcul fonctionnel
- Opérateurs maximaux
- Espaces Lp non-commutatifs
- Espaces d’opérateurs
- Transformées de Riesz
- Intégrales singulières
- Geometrie des espaces de Banach
- Multiplicateurs de Fourier sur des groupes et multiplicateurs de Schur
- R-bornitude
3 Présentation du projet
Depuis les travaux fondamentaux de Stein et Cowling, la théorie spectrale
des semigroupes est devenue un sujet mathématique large et beaucoup de
mathématiciens y travaillent aujourd’hui. Beaucoup de progrès a été obtenu pendant
les quatre dernières décennies, beaucoup de belles connections se sont avérées
fructueuses pour résoudre des problèmes dans l’analyse harmonique et autour. Le
but du projet HASCON est de répondre aux questions suivantes qui émergent dans
le contexte de théorie spectrale, calcul fonctionnel, analyse harmonique ou équations
aux dérivées partielles abstraites :
- Sous quelles conditions (p.ex. quel espace Lp ou de Banach classique
ou non-commutatif soujacent) un générateur d’un semigroupe admet-il
un calcul H∞ ou un calcul fonctionnel de type Hormander-Mihlin?
Cette propriété est connue d’être de grande importance dans des aspects
théoriques et pour beaucoup d’applications. La réponse dépend de
l’espace soujacent X, qui peut être composé de fonctions sur un espace
mesuré Ω (souvent Lp(Ω), ou également un espace Lp non-commutatif,
c’est-à-dire un espace qui consiste d’opérateurs (non) bornés affiliés à une
algèbre de von Neumann). Ici des propriétés géométriques de l’espace
de Banach X jouent typiquement un rôle important, et nous mettons
une attention particulière à des espaces de Bochner X = Lp(Ω,Y ).
Alors la propriété de Y d’être un espace UMD devient importante et de
même son type et cotype de Rademacher ainsi que des notions reliées
comme p-convexité et q-concavité si Y est de plus un treillis. Notre
motivation pour des espaces de Bochner provient de leur importance dans
des applications à des problèmes abstraits de Cauchy, où Y reprend le rôle
d’une variable spatiale, alors que la variable temporelle est le paramètre
t du semigroupe Tt ; importance pour des estimations de fonctions
carrées, où Y = ℓ2 (alors la question intéressante de calcul fonctionnel
fait intervenir une suite de multiplicateurs spectraux (fk)k); et puis
importance pour la description d’espaces de fonctions abstraits associés
au générateur, tel que des espaces de Sobolev et Triebel-Lizorkin, où
Y = ℓq.
- Dans quels cas un opérateur maximal d’évolution, dans la forme la plus
classique MTf = supt>0|Ttf| ou opérateur maximal spatial MHLf =
supr>0
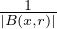 ∫
B(x,r)|f(y)|dy est-il borné? Cette question et le calcul
fonctionnel ci-dessus sont fortement liés et se renforcent mutuellement.
Ainsi, d’un côté, un calcul H∞ avec un bon angle permet d’étendre
la bornitude de l’opérateur maximal d’evolution sur Lp(Ω) ci-dessus à
un opérateur maximal sectoriel. Ensuite sous la présence d’estimation
de noyau d’intégrale de Tt, les opérateurs maximaux d’évolution et
spatial sont simultanément bornés. D’un autre côté, la bornitude d’un
opérateur maximal est parfois un outil clé pour établir un calcul H∞
et Hormander-Mihlin. Encore une fois, nous mettons une attention
particulière à la bornitude de MHL,MT dans des espaces de Bochner.
D’un point de vue général, les opérateurs maximaux standard sont
importants dans plusieurs branches d’analyse harmonique et réelle (p.ex.
intégrales singulières, multiplicateurs, théorie de Littlewood-Paley).
∫
B(x,r)|f(y)|dy est-il borné? Cette question et le calcul
fonctionnel ci-dessus sont fortement liés et se renforcent mutuellement.
Ainsi, d’un côté, un calcul H∞ avec un bon angle permet d’étendre
la bornitude de l’opérateur maximal d’evolution sur Lp(Ω) ci-dessus à
un opérateur maximal sectoriel. Ensuite sous la présence d’estimation
de noyau d’intégrale de Tt, les opérateurs maximaux d’évolution et
spatial sont simultanément bornés. D’un autre côté, la bornitude d’un
opérateur maximal est parfois un outil clé pour établir un calcul H∞
et Hormander-Mihlin. Encore une fois, nous mettons une attention
particulière à la bornitude de MHL,MT dans des espaces de Bochner.
D’un point de vue général, les opérateurs maximaux standard sont
importants dans plusieurs branches d’analyse harmonique et réelle (p.ex.
intégrales singulières, multiplicateurs, théorie de Littlewood-Paley).
- Quel type d’opérations sur un espace Lp non-commutatif produit
des applications bornées et complètement bornées? Les exemples les
plus éminents de telles applications qui sont importantes en analyse
harmonique sont des multiplicateurs de Schur, des multiplicateurs de
Fourier non-commutatifs ou des opérations provenantes de la seconde
quantisation, tels que les semigroupes de q-Ornstein-Uhlenbeck. Les
multiplicateurs de Schur fournissent une classe surprenamment riche
d’applications et sont utilisés depuis longtemps dans des domaines
variés en analyse tels que l’analyse complexe, les espaces de Banach, la
théorie des opérateurs, l’analyse multivariée, la théorie des opérateurs
absolument sommants et le calcul fonctionnel. Les multiplicateurs de
Fourier sur des groupes non-commutatifs et la seconde quantisation
sont des domaines plutot récents en analyse harmonique. L’analyse
harmonique non-commutative fait intervenir plus de structure algébrique
et combinatoire.
4 Évènements
Les Jeudi 20 octobre - Vendredi 21 octobre 2022 a eu lieu la rencontre à l’université
Paris-Est Marne-la-Vallée intitulée
Harmonic Analysis of semigroups on commutative and non-commutative Lp
spaces.
Le thème de cette rencontre étaient des techniques en analyse harmonique qui
s’appliquent avec succès dans la théorie Lp des opérateurs (calcul fonctionnel,
semigroupes d’opérateurs, opérateurs maximaux, fonctions carrées) – et
récemment ont pu être adapté dans un contexte non-commutatif tel que
des multiplicateurs de Fourier sur des groupes localement compacts et des
multiplicateurs de Schur. Il y avait quatre + sept exposés de 60 min + 30 min
et comme coutume du temps pour des discussions. Le programme était le
suivant.
| | Jeudi 20 Octobre 2022 |
| 9h00 – 9h30 | Reception des participants au LAMA = pause café 1 |
| 9h30 –10h30 | Wolfgang Arendt |
| 10h45 – 11h45 | Mariusz Mirek |
| 12h00 – 14h00 | Déjeuner |
| 14h00 –14h30 | Blazej Wróbel |
| 14h30 – 15h00 | Oliver Dragičević |
| 15h00 – 15h30 | Pause café 2 |
| 15h30 – 16h00 | Emiel Lorist |
| 16h00 – 16h30 | Nick Lindemulder |
| 16h30 – 17h00 | Tomasz Szarek |
| 20h00 | Dîner de la conférence |
| | Vendredi 21 Octobre 2022 |
| 09h30 – 10h30 | El Maati Ouhabaz |
| 10h30 – 11h00 | Pause café 3 |
| 11h00 – 11h30 | Cédric Arhancet |
| 11h30 – 12h00 | Léonard Cadilhac |
| 12h00 – 14h00 | Déjeuner 2 |
| 14h00 – 15h00 | Mark Veraar |
Voici la liste des participants à jour le 28/09/2022.
- Benjamin Arras
- Sebastian Bechtel
- Clément Coine
- Lukas Hagedorn
- Kamal Khalil
- Fatima Zahra Lahbriri
- Christian Le Merdy
- Éric Ricard
- Silvia Romanelli
- Elizabeth Strouse
- Alexandre Thorel
- Safoura Zadeh
5 Publications and Preprints
- L. Deléaval et C. Kriegler : Dunkl spectral multipliers with values in
UMD lattices, Journal of Functional Analysis, 272(5) :2132–2175, 2017.
Préprint ici et sur HAL.
- L. Deléaval et C. Kriegler : Dimension free bounds for the vector-valued
Hardy-Littlewood maximal operator, Rev. Mat. Iberoam., 35(1) :101–123,
2019. Préprint sur HAL, arxiv.org.
- L. Deléaval, M. Kemppainen et C. Kriegler : Hörmander functional
calculus on UMD lattice valued Lp spaces under generalised Gaussian
estimates, Journal d’Analyse Mathématique, 145(1), 177–234, 2021.
Préprint ici, sur HAL et sur arXiv.org.
- C. Arhancet et C. Kriegler : Complementation of the subspace of
radial multipliers in the space of Fourier multipliers on ℝn, Archiv der
Mathematik, 112(1), 93–100, 2019. Préprint sur HAL, arXiv.org.
- C. Arhancet et C. Kriegler : Projections, multipliers and decomposable
maps on noncommutative Lp-spaces, Mémoires de la Société
Mathématique de France, 177 (new series). Préprint sur HAL et sur
arXiv.org.
- C. Arhancet et C. Kriegler : Riesz transforms, Hodge-Dirac operators
and functional calculus for multipliers, Springer Lecture Notes in
Mathematics, 2304. Springer, 2022, Cham, xii+278 pp. Préprint sur HAL
et sur arXiv.org.
- C. Arhancet : Dilations of markovian semigroups of Fourier multipliers
on locally compact groups, Préprint sur arXiv.org.
- K. Domelevo, C. Kriegler et S. Petermichl : H∞ calculus for
submarkovian semigroups on weighted L2 spaces Mathematische
Annalen, 381(3-4), 1137–1195, 2021. Préprint sur HAL et arXiv.org.
- C. Arhancet : Positive contractive projections on noncommutative
Lp-spaces and nonassociative Lp-spaces, Préprint sur arXiv.org.
- C.
Arhancet : Contractively decomposable projections on noncommutative
Lp-spaces, Préprint sur arXiv.org.
- C. Arhancet : Dilations of markovian semigroups of measurable Schur
multipliers, Préprint sur arXiv.org.
- J. Conde-Alonso, A. González-Pérez et J. Parcet : Noncommutative
strong maximals and almost uniform convergence in several directions,
Forum Math. Sigma 8, Paper No. e57, 39 p. (2020). Préprint sur
arXiv.org.
- L. Deléaval, N. Demni : Generalized Bessel functions of dihedral-type:
expression as a series of confluent Horn functions and Laplace-type
integral representation, Ramanujan J. 54, No. 1, 197-217 (2021).
- S. Ben Saïd. and L. Deléaval : Translation operator and maximal
function for the (k,1)-generalized Fourier transform, J. Funct. Anal. 279,
No. 8, Article ID 108706, 31 p. (2020).
- C.
Arhancet : Contractively decomposable projections on noncommutative
Lp-spaces, Préprint sur arXiv.org, soumis.
- C. Arhancet et Yves Raynaud : 2-positive contractive projections on
noncommutative Lp-spaces, soumis.
- C. Arhancet : A characterization of completely bounded normal Jordan
*-homomorphisms on von Neumann algebras, soumis.
- C. Arhancet : Quantum information theory and Fourier multipliers on
quantum groups, submitted, Préprint sur arxiv.org.
- L. Deléaval et C. Kriegler : Maximal Hörmander Functional Calculus
on Lp spaces and UMD lattices, International Mathematical Research
Notices, Préprint sur HAL, sur arXiv.org et ici.
- C. Arhancet : Dilations of semigroups on von Neumann algebras and
noncommutative Lp-spaces, J. Funct. Anal., 276, No. 7, 2279-2314
(2019).
- L. Deléaval et C. Kriegler : q-variational Hörmander functional calculus
and Schrödinger and wave maximal estimates, Préprint ici.
- C. Arhancet, C. Kriegler, C. Le Merdy et S. Zadeh : Separating Fourier
and Schur multipliers. Accepté pour publication dans Journal of Fourier
Analysis and Applications. Préprint sur HAL et sur arXiv.org.
- C. Arhancet et C. Kriegler : Fourier-Stieltjes algebras, decomposable
Fourier multipliers and amenability. Préprint sur arXiv.org.
- A. González-Pérez : Lower bounds in Lp-transference for crossed
products. Préprint sur arXiv.org.
- A. González-Pérez, J. Parcet et R. Xia : Noncommutative Cotlar
identities for groups acting on tree-like structures. Préprint sur arXiv.org.
- S. Ben Saïd et L. Deléaval : A Hardy-Littlewood maximal operator
for the generalized Fourier transform on ℝ. J. Geom. Anal. 30, No. 2,
2273-2289 (2020).
- C. Arhancet : Spectral triples, Coulhon-Varopoulos dimension and heat
kernel estimates. Soumis. Préprint sur arXiv.org.
- C. Arhancet : Sobolev algebras on Lie groups and noncommutative
geometry. Soumis. Préprint sur arXiv.org.
Page mis à jour le 01/02/2024.



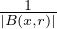 ∫
B(x,r)|f(y)|dy est-il borné? Cette question et le calcul
fonctionnel ci-dessus sont fortement liés et se renforcent mutuellement.
Ainsi, d’un côté, un calcul H∞ avec un bon angle permet d’étendre
la bornitude de l’opérateur maximal d’evolution sur Lp(Ω) ci-dessus à
un opérateur maximal sectoriel. Ensuite sous la présence d’estimation
de noyau d’intégrale de Tt, les opérateurs maximaux d’évolution et
spatial sont simultanément bornés. D’un autre côté, la bornitude d’un
opérateur maximal est parfois un outil clé pour établir un calcul H∞
et Hormander-Mihlin. Encore une fois, nous mettons une attention
particulière à la bornitude de MHL,MT dans des espaces de Bochner.
D’un point de vue général, les opérateurs maximaux standard sont
importants dans plusieurs branches d’analyse harmonique et réelle (p.ex.
intégrales singulières, multiplicateurs, théorie de Littlewood-Paley).
∫
B(x,r)|f(y)|dy est-il borné? Cette question et le calcul
fonctionnel ci-dessus sont fortement liés et se renforcent mutuellement.
Ainsi, d’un côté, un calcul H∞ avec un bon angle permet d’étendre
la bornitude de l’opérateur maximal d’evolution sur Lp(Ω) ci-dessus à
un opérateur maximal sectoriel. Ensuite sous la présence d’estimation
de noyau d’intégrale de Tt, les opérateurs maximaux d’évolution et
spatial sont simultanément bornés. D’un autre côté, la bornitude d’un
opérateur maximal est parfois un outil clé pour établir un calcul H∞
et Hormander-Mihlin. Encore une fois, nous mettons une attention
particulière à la bornitude de MHL,MT dans des espaces de Bochner.
D’un point de vue général, les opérateurs maximaux standard sont
importants dans plusieurs branches d’analyse harmonique et réelle (p.ex.
intégrales singulières, multiplicateurs, théorie de Littlewood-Paley).